Gauß ohne Schrecken: so funktioniert das Rechnen mit der Normalverteilung (Teil 2-3)

Im vorigen Artikel dieser kleinen Serie haben wir demonstriert, wie die gauß'sche Dichtefunktion grundsätzlich funktioniert. In diesem Artikel läuten wir erstmals die gauß'sche Glockenkurve – an einem materialwirtschaftlichen Beispiel. Der Leser sollten die zugrundeliegende Tabelle zur Hand haben, um der Rechnung folgen zu können.

Im bereits eingeführten Beispiel waren wir davon ausgegangen, daß die – als normalverteilt angenommene – Nachfrage nach einem Artikel durchschnittliche pro Tag 500 Stück bei einer Standardabweichung von Sigma ± 60 Stück betrage. Das ist zunächst noch etwas theoretisch. Der Lagerbetreiber habe aber nur Lagerraum für maximal 600 Produkte pro Tag. Es kann nur ein Mal pro Tag angeliefert werden. Wenn also mehr als 600 Stück nachgefragt werden, so tritt Lieferunfähigkeit ein, weil das Lager leer ist. Wie groß ist das Risiko, daß dies passiert?

Die Normalisierung

Dies kann mit der gauß'schen Normalverteilungsfunktion berechnet werden, aber man muß erst die Stück in Sigmas umrechnen. Dieser Vorgang heißt Normalisierung. Soll ein Grenzwert i.H.v. Xmax = 600 Stück berechnet werden, so ist hiervon der Mittelwert von 500 Stück abzuziehen und diese Differenz durch den Wert eines Sigmas zu teilen:

Die Grenze der Lagerkapazität i.H.v. Xmax = 600 Stück liegt also bei Mittelwert + 1,67 Standardabweichungen. Der Bereich oberhalb dieser Grenze ist das Risiko der Lieferunfähigkeit, das dem Flächenanteil des markierten Teiles der Kurve an der ganzen Kurve entspricht: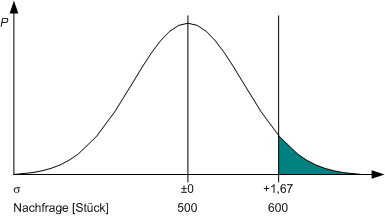

So, und jetzt läuten wir die gauß'sche Glocke, und das geht ganz einfach: wir schlagen in der bekannten Tabelle den Wert für 1,67 Sigma nach und finden einer Wahrscheinlichkeit i.H.v. 45,25403%. Dies ist die Wahrscheinlichkeit einer Nachfrage zwischen 500 und 600 Stück. Wir wollen aber wissen, wie hoch die Wahrscheinlichkeit ist, über 600 Stück pro Tag zu liegen. Also ziehen wir den Ergebniswert aus der Tabelle einfach von eienr Hälfte der Kurve, also von 50% ab, und erhalten für das Risiko der Lieferunfähigkeit einen Wert von 4,74597%.

Dieses war der erste gauß'sche Glockenschlag: das Auffinden der Wahrscheinlichkeit zu einem gegebenen Grenzwert. Im nächsten und letzten Beitrag dieser Serie schauen wir uns das gegenteil an: wie findet man den Grenzwert, wenn ein (maximales) Risikoniveau gegeben ist?

Links zum Thema: Gauß ohne Schrecken: so funktioniert das Rechnen mit der Normalverteilung (Teil 1-3) | Tabelle der gauß'schen Normalverteilung | Gauß-Rechner für Excel | Formelsammlung der Betriebswirtschaft (interne Links)

Hinweise auf relevante Inhalte der BWL CD: [Lexikon]: "Arithmetisches Mittel", "geometrisches Mittel", "Marktforschung", "Mittelwert", "Normalverteilung", "Standardabweichung", "Verteilungsart". [Manuskripte]: "Formelsammlung der BWL.pdf", "Marktforschung.pdf", "Statistik Skript.pdf". [Excel]: "Gauß'sche Normalverteilung.xls", "Varianz.xls".
Diese Hinweise beziehen sich auf die zum Zeitpunkt des Erscheinens dieses Artikels aktuelle Version der BWL CD. Nicht alle Inhalte und nicht alle Stichworte sind in älteren Fassungen enthalten. Den tagesaktuellen Stand ersehen Sie aus dem Inhaltsverzeichnis oder dem thematischen Verzeichnis.